如果一个有向图或无向图存在一笔画（不重复路径的一笔画完所有顶点和边），则一笔画的路径叫做欧拉路。如果最后又回到了起点，那这个路径叫欧拉回路。

一、欧拉路和欧拉回路

• 欧拉路径是指从图中一个点开始到图中一个点结束的路径，并且图中每条边通过的且只通过一次（顶点可以多次）。一个图可以有多条欧拉路径。

• 欧拉回路是欧拉回路是指起点和终点相同的欧拉路。

我们定义奇点是指跟这个点相连的边的数目有奇数个的点。对于一笔画的图，有以下两个定理：

定理1：存在欧拉路的条件：图是连通的，有且只有2个奇点；

定理2：存在欧拉回路的条件：图是连通的，有0个奇点。

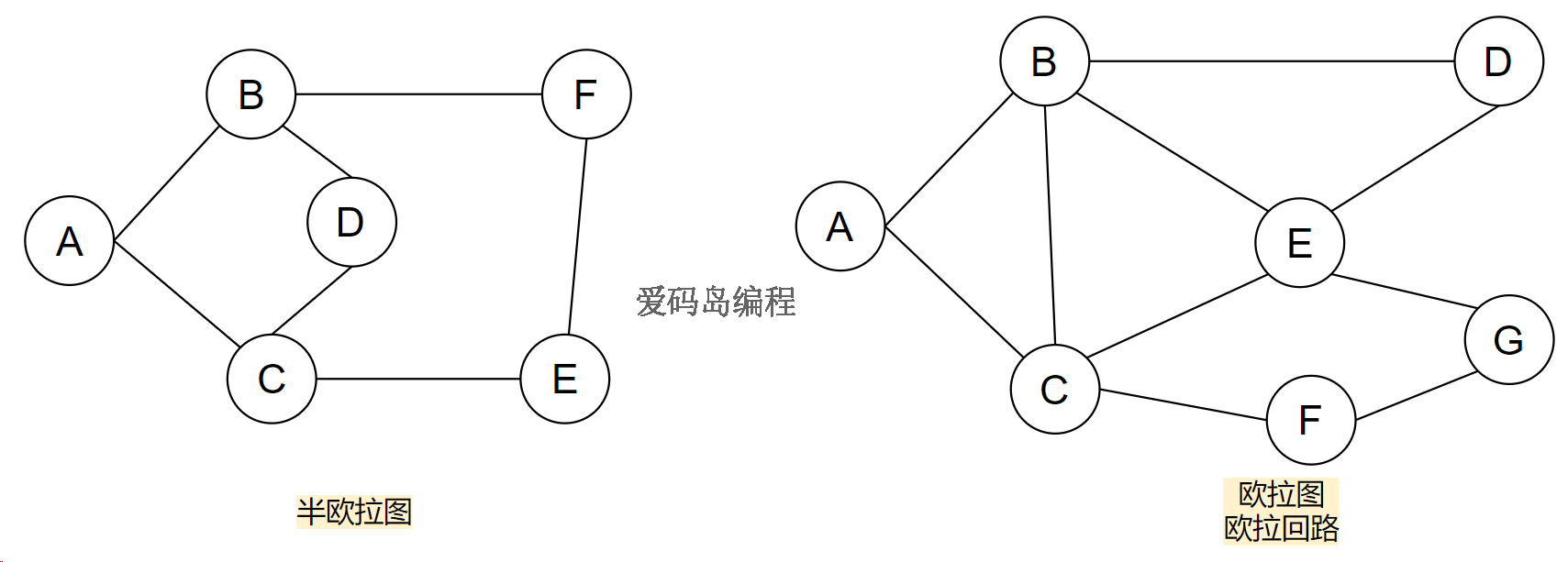
二、欧拉图和半欧拉图

具有欧拉回路的图叫欧拉图，不具有欧拉回路的图叫半欧拉图。

这两个定理是显而易见的，既然每条边都要经过一次，那么对于欧拉路，除了起点和终点外，每个点如果要进入一次，显然一定要出去一次，显然是偶点。对于欧拉回路，每个点进入和出去的次数一定是相等的，显然没有奇点。

欧拉图：对于无向图来说，所有顶点的度都是偶数；对于有向图来说，所有顶点的入度和出度相等。

半欧拉图：对于无向图来说，有且仅有两个顶点的度为奇数；对于有向图来说，有且仅有一个顶点入度-出度=1，另有且仅有一个顶点出度-入度=1。

三、如何找到欧拉路

1、先判断是有向图还是无向图；

• 无向图：

  • 欧拉图：所有顶点的度都是偶数

  • 半欧拉图：有且仅有两个顶点的度为奇数

• 有向图

  • 欧拉图：所有顶点的入度和出度相等

  • 半欧拉图：有且仅有一个顶点入度-出度=1，另有且仅有一个顶点出度-入度=1

2、求欧拉路的算法使用深度优先遍历，每经过一条边，就把这条边设置visited。

• 如下图：首先是无向图，然后统计图的结点的度都是偶数，那么就是欧拉图；

• 找到一个奇数条边的点作为起点，如果没有找到就随便找一个点作为起点；

• 针对边进行DFS递归搜索，访问所有未访问过的边；

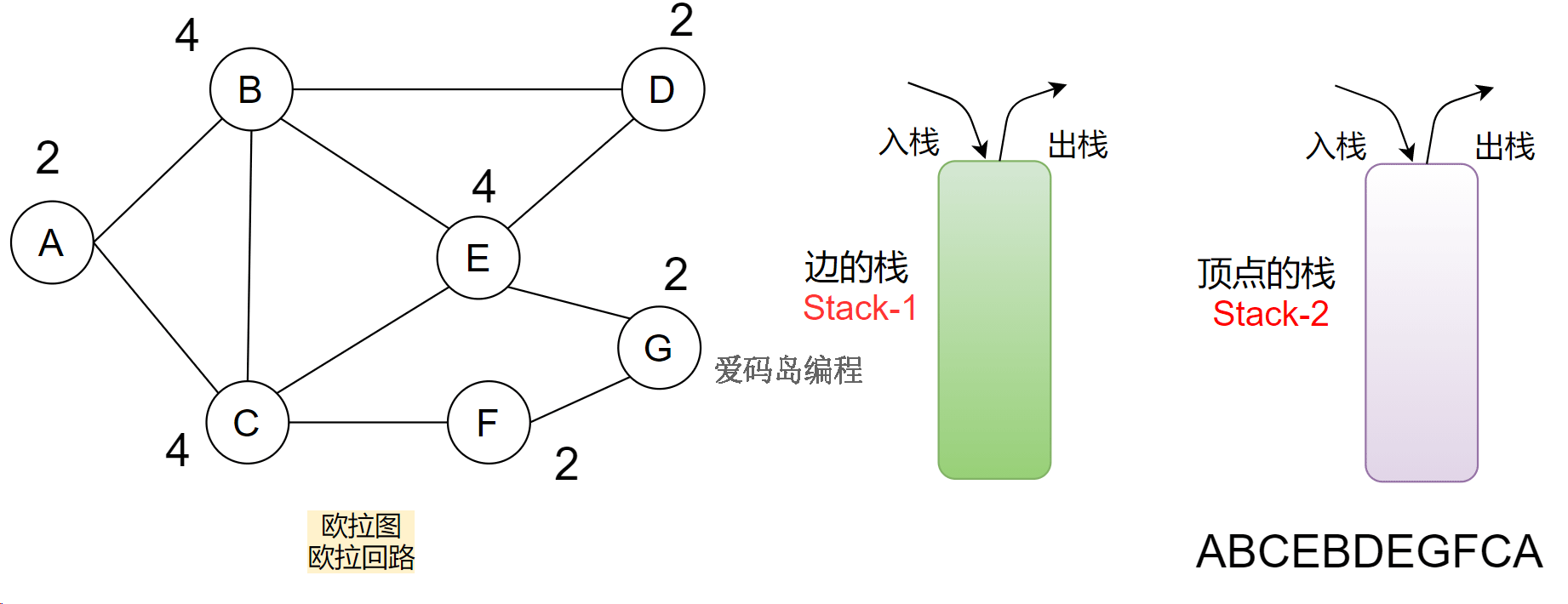
3、针对边的深度优先遍历过程如下：

• A点为起点，AB这条边入栈Stack-1，也就是：A入栈、B入栈；（AB边被访问过visited）

• B点为起点，BC这条边入栈，也就是：C入栈；（BC边visited）

• C点为起点，CA这条边入栈，也就是：A入栈；（CA边visited）

• A点为起点，所有的边都被访问过，那么A点出栈，进入Stack-2

• 回溯到C点，CE这条边入栈，也就是：E入栈；（CE边visited）

• E点为起点，EB这条边入栈，也就是：B入栈；（EB边visited）

• B点为起点，BD这条边入栈，也就是：D入栈；（BD边visited）

• D点为起点，DE这条边入栈，也就是：E入栈；（DE边visited）

• E点为起点，EG这条边入栈，也就是：G入栈；（EG边visited）

• G点为起点，GF这条边入栈，也就是：F入栈；（GF边visited）

• F点为起点，FC这条边入栈，也就是：C入栈；（FC边visited）

• C点为起点，所以边都被访问过，那么C点出栈，进入Stack-2

• 依次是F、G、E、D、B、E、C、B、A出栈Stack-1，入栈Stack-2

• Stack-2中的元素是（栈底到栈顶）：A、C、F、G、E、D、B、E、C、B、A

• Stack-2出栈：ABCEBDEGFCA

ABCEBDEGFCA 就是欧拉回路，尝试一下，可以一笔画完。

三、练习题

欧拉图G是指可以构成一个闭回路的图，且图G的每一条边恰好在这个闭回路上出现一次(即一笔画)。以下各个描述中，不一定是欧拉图的是( )

A. 图G中没有度为奇数的顶点

B. 包括欧拉环游的图（欧拉环游图是指通过图中每边恰好一次的闭路径）

C. 包括欧拉闭迹的图（欧拉迹是指通过图中每边恰好一次的路径）

D. 存在一条回路，通过每个顶点恰好一次

参考答案 D

参考欧拉图的定义。