图是非常复杂的非线性结构。在人工智能、工程、数学、物理、计算科学等领域,有非常广泛的应用。存储时通常用邻接矩阵来表示图的结构。邻接矩阵是数学和计算机科学中常用的一种表示方式,比如用来表述有向图或无向图。
对于图而言,是数据结构中最复杂的结构了,而实际做题过程中,最大的难点在于广度优先搜索和深度优先搜索的过程。
图从两个维度划分,可以分为:有向图和无向图、无权图和带权图。(联想到火车站点、城市交通等)

一、图的概念
图(Graph)是由两个集合V和E组成的,记为:G=(V,E),其中:V是顶点的有穷非空集合,E是V中顶点的偶对(称为边)的有穷集合。通常也将图G的顶点集和边集分别记为V(G)和E(G),E(G)可以是空集,表示图只有顶点而没有边。

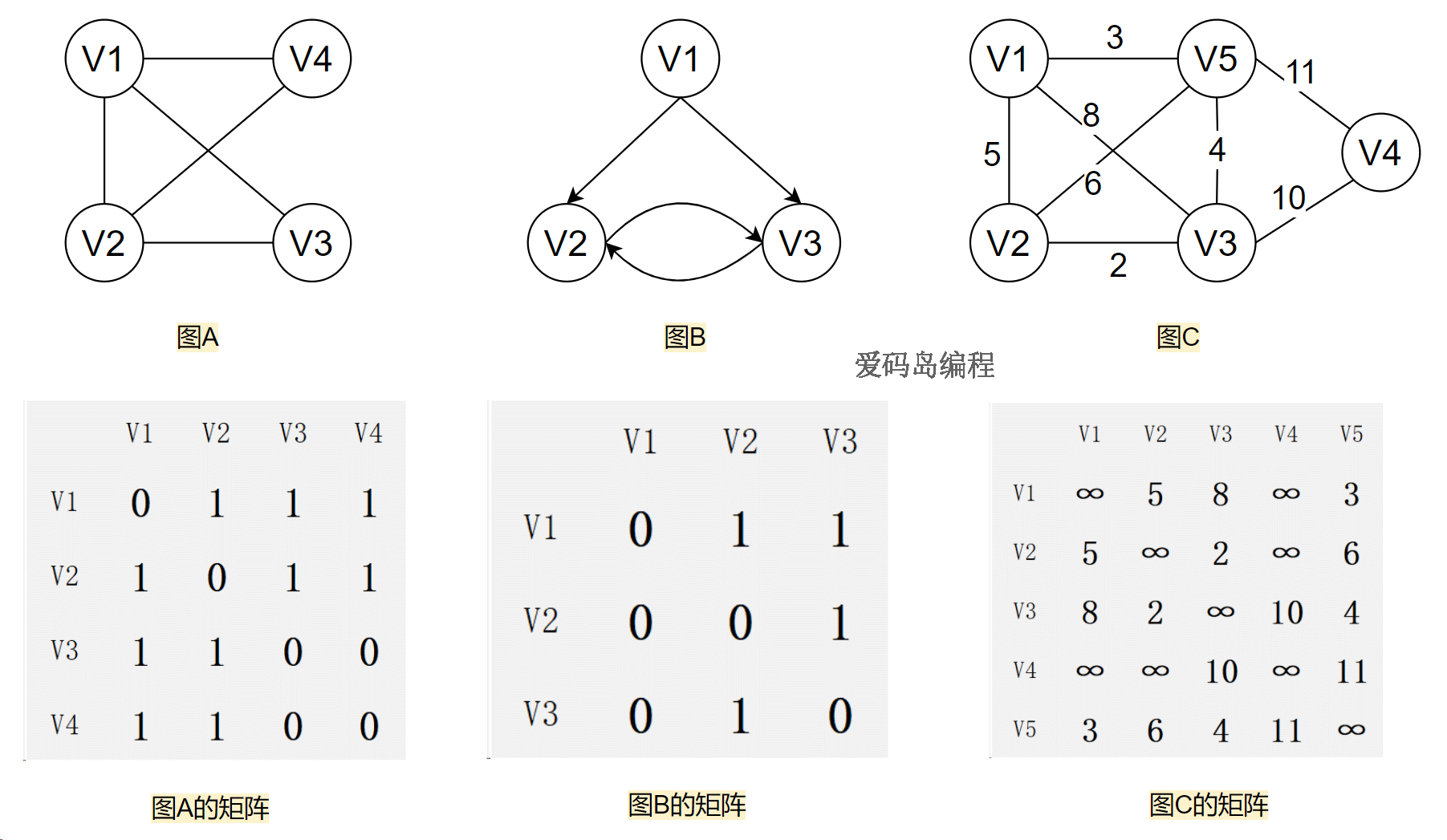
有向图(Directed Graph):图的边有方向,只能按箭头方向从一点到另外一点。
无向图(Undirected Graph):图是边没有方向(无箭头),表示双向关系。
结点的度:无向图中与结点相连的边的数目,称为结点的度。如无向图中结点B的度是4。
结点的入度:在有向图中,以这个结点为终点的有向边的数目。如有向图中结点B的入度的3。
结点的出度:在有向图中,以这个结点为起点的有向边的数目。如有向图中结点B的出度是1。
联通性:如果图中结点U、V之间存在一条从U通过若干个顶点、边到达V的通路,则称U和V是联通的。
权值:与边相关联的值。权值可以表示很多意义,如距离、时间、成本等等,取决于你要解决的问题,比如,在导航用中,每结点可以代表一个地点,边的权值就可以代表两个地点之间的距离。在这种情况下,既要统计边的数量,还要计算边的权值。
回路:起点和终点相同的路径,称为回路,或环。比如无向图的 A-B-C;有向图的B-E-D。
完全图:一个n阶(顶点)的完全有向图含有 n*(n-1) 条边;一个n阶的完全无向图含有 n*(n-1)/2 条边。
强联通分量:有向图中任意两点都连通的最大子图。比如 有向图的 B-E-D。
二、图的存储结构
用二维数组邻接矩阵存储。
对于邻接矩阵而言,不需要去考虑是有向的还是无向的,统一都可以理解成有向的,因为有向图可以兼容无向图,对于无向图而言,只不过这个矩阵按照主对角线是对称的,因为A到B有边,则必然B到A也有边。
G[101][101];
G[i][j] 的值,表示从点 i 到点 j 的边的权值,定义如下:
1、G[i][j] 是 1 或者权值:表示 Vi 到 Vj 之间有边,取值为1或权值。
2、G[i][j] 是 0 或者∞:表示 Vi 到 Vj 之间无边,取值为0或∞(无穷大)。
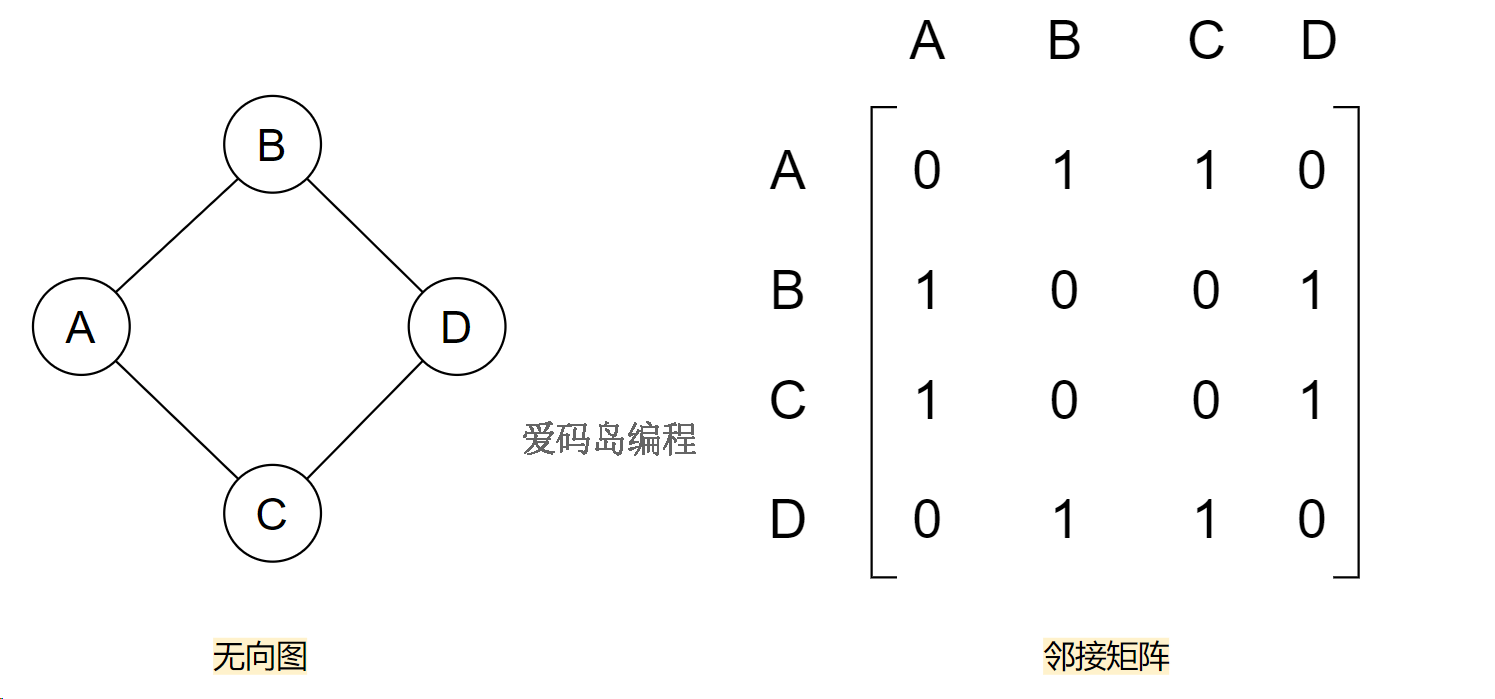
三、图的存储的几个案例