二叉树遍历

数据结构和算法

二叉树遍历

阅读量: 219 编辑

二叉树的遍历是指从根结点出发，按照某种顺序依次访问二叉树中的所有结点，使得每个结点访问一次且仅被访问一次。

二叉树遍历方法：前序遍历、中序遍历、后序遍历、层序遍历

struct TreeNode{
    char data;
    TreeNode *left;
    TreeNode *right;
};

一、先序遍历

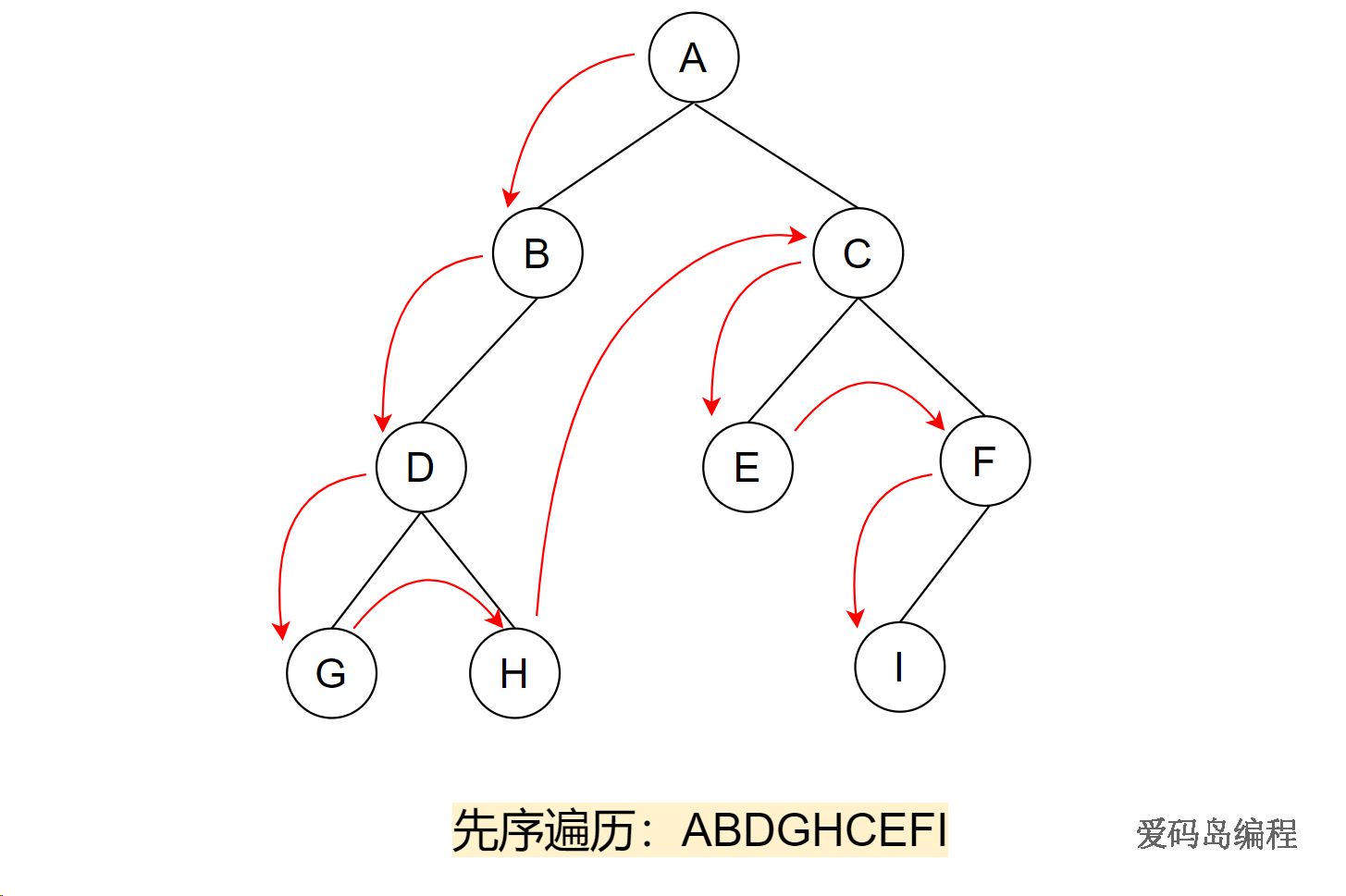
如果二叉树为空则直接返回。否则先访问根结点，再递归先序遍历左子树，再递归先序遍历右子树。

它的递归遍历顺序是：访问根结点—先序遍历左子树—先序遍历右子树

先访问根结点A；递归遍历A的左子树B；递归遍历B的左子树D；递归遍历D的左子树G；
G没有左子树了，访问G；
递归遍历D的右子树H；H没有左子树，也没有右子树，访问H；
返回到B；B没有右子树；返回到A；
A有右子树；递归遍历右子树C；递归遍历C的左子树E；E没有孩子结点，访问E；
再递归遍历C的右子树F，访问根结点F；
F有左子树I，访问I；
没有右子树；结束递归遍历。

void PreOrderTraverse(TreeNode *root) {
    if(root == NULL) {
        return;
    }
    
    print(root->data);//访问数据
	PreOrderTraverse(root->left);//递归遍历
	PreOrderTraverse(root->right);
}

二、中序遍历

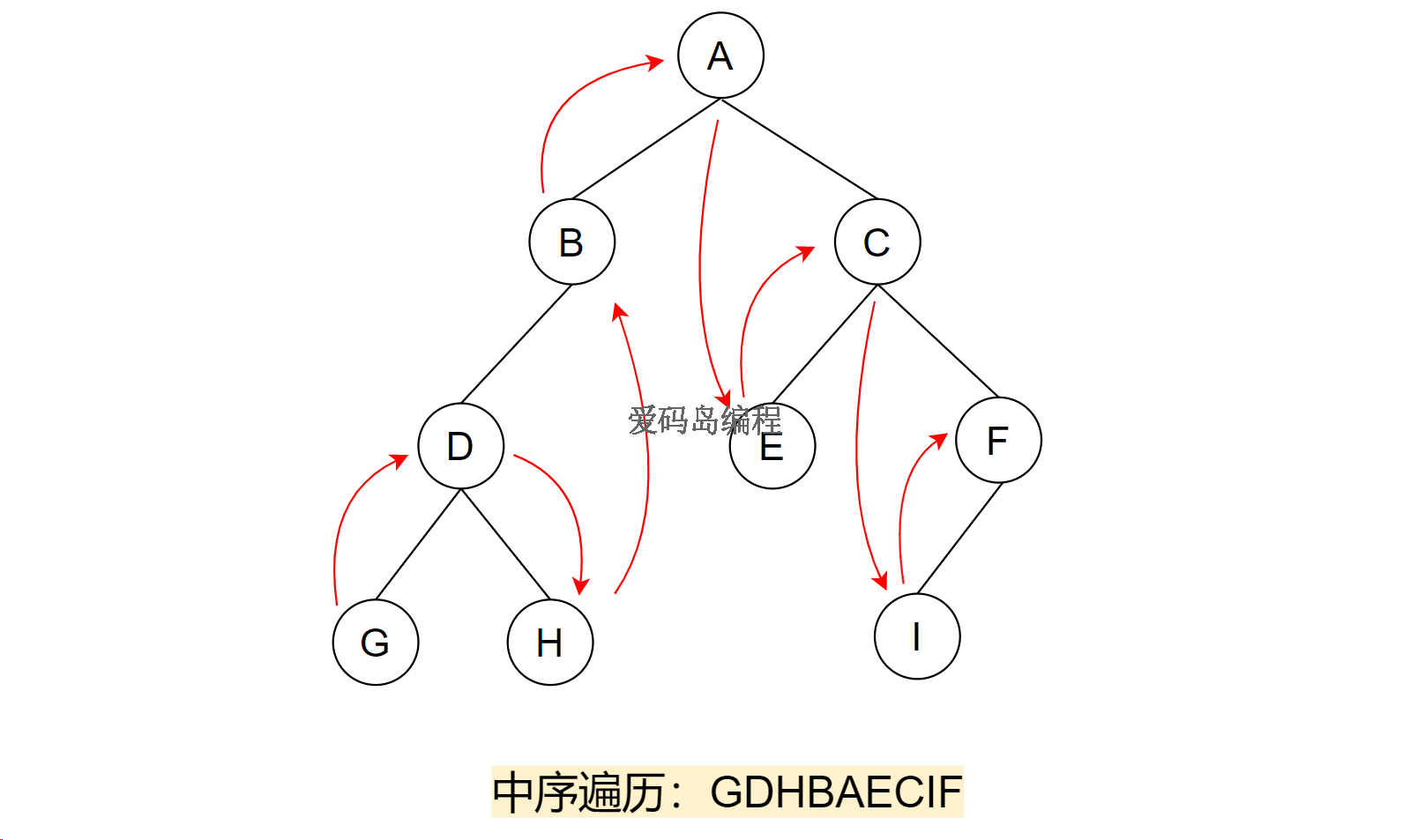
如果二叉树为空则直接返回。否则先递归中序遍历左子树，再访问根结点，再递归中序遍历右子树。

它的递归遍历顺序是：左子树—根结点—右子树

递归左子树，G没有孩子结点，访问G；
访问G的根结点D；
递归遍历D的右子树H；没有孩子结点，访问H；
访问B结点；
递归遍历B的右子树，为空；
访问A结点；
递归遍历A的右子树，递归找到了E，访问E；
访问E的根结点C；
递归遍历C的右子树F；F有左子树，递归找到了I，访问I；
访问I的根结点F；
递归结束；

void InOrderTraverse(TreeNode *root) {
    if(root == NULL) {
        return;
    }
    
	InOrderTraverse(root->left);//递归遍历
    print(root->data);//访问
	InOrderTraverse(root->right);
}

三、后序遍历

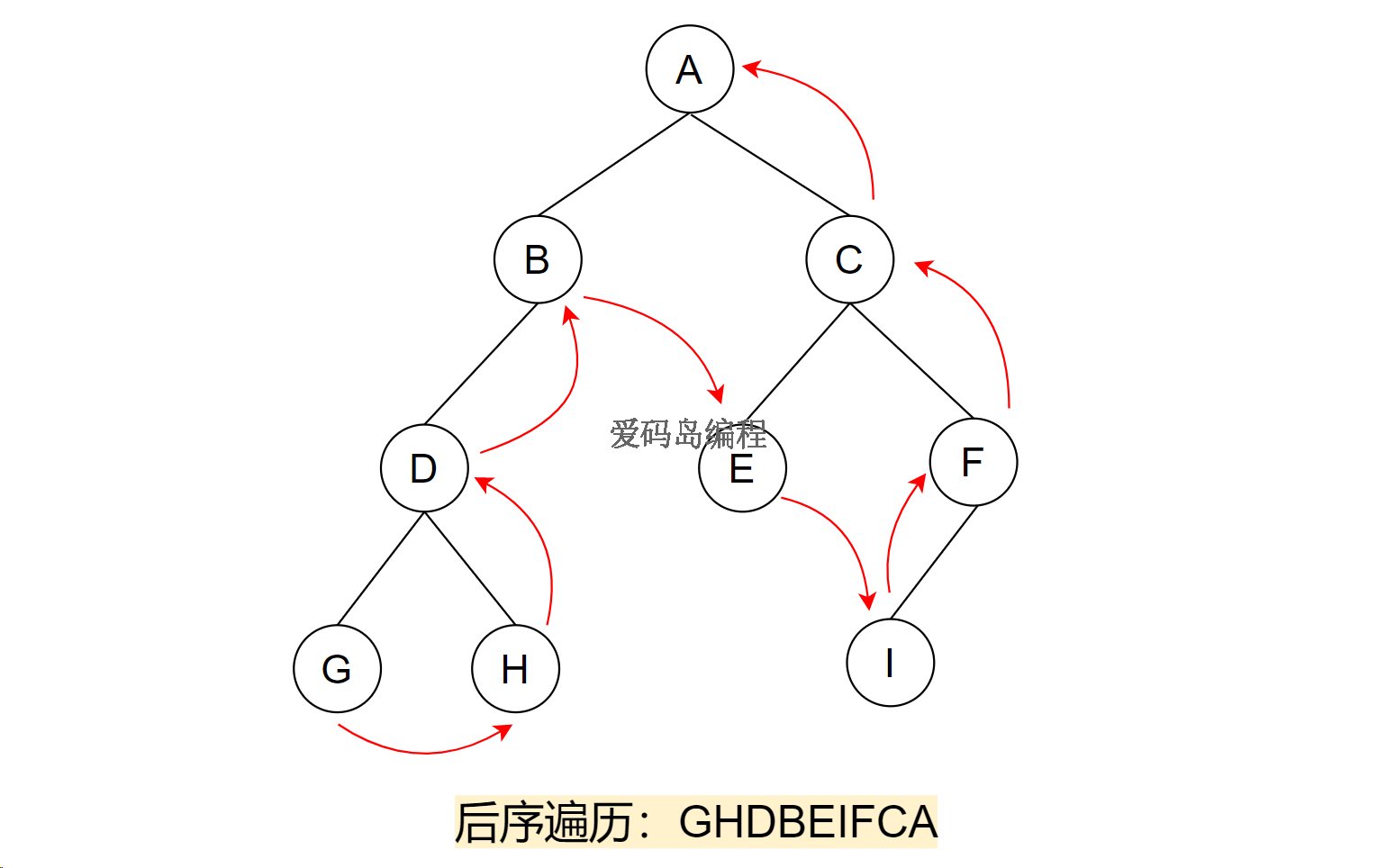
如果二叉树为空则直接返回。否则先递归后序遍历左子树，再递归后序遍历右子树，再访问根结点。

它的递归遍历顺序是：左子树—右子树—根结点

递归左子树，G没有孩子结点，访问G；
递归遍历D的右子树H；没有孩子结点，访问H；
访问根结点D；
递归遍历B的右子树，为空；
访问B结点；
递归遍历A的右子树，递归找到了E，访问E；
递归遍历C的右子树F；F有左子树，递归找到了I，访问I；
访问I的根结点F；
访问C；访问A；
递归结束；

void PostOrderTraverse(TreeNode *root) {
    if(root == NULL) {
        return;
    }
    
	PostOrderTraverse(root->left);//递归遍历
	PostOrderTraverse(root->right);
    print(root->data);//访问结点
}

四、层序遍历

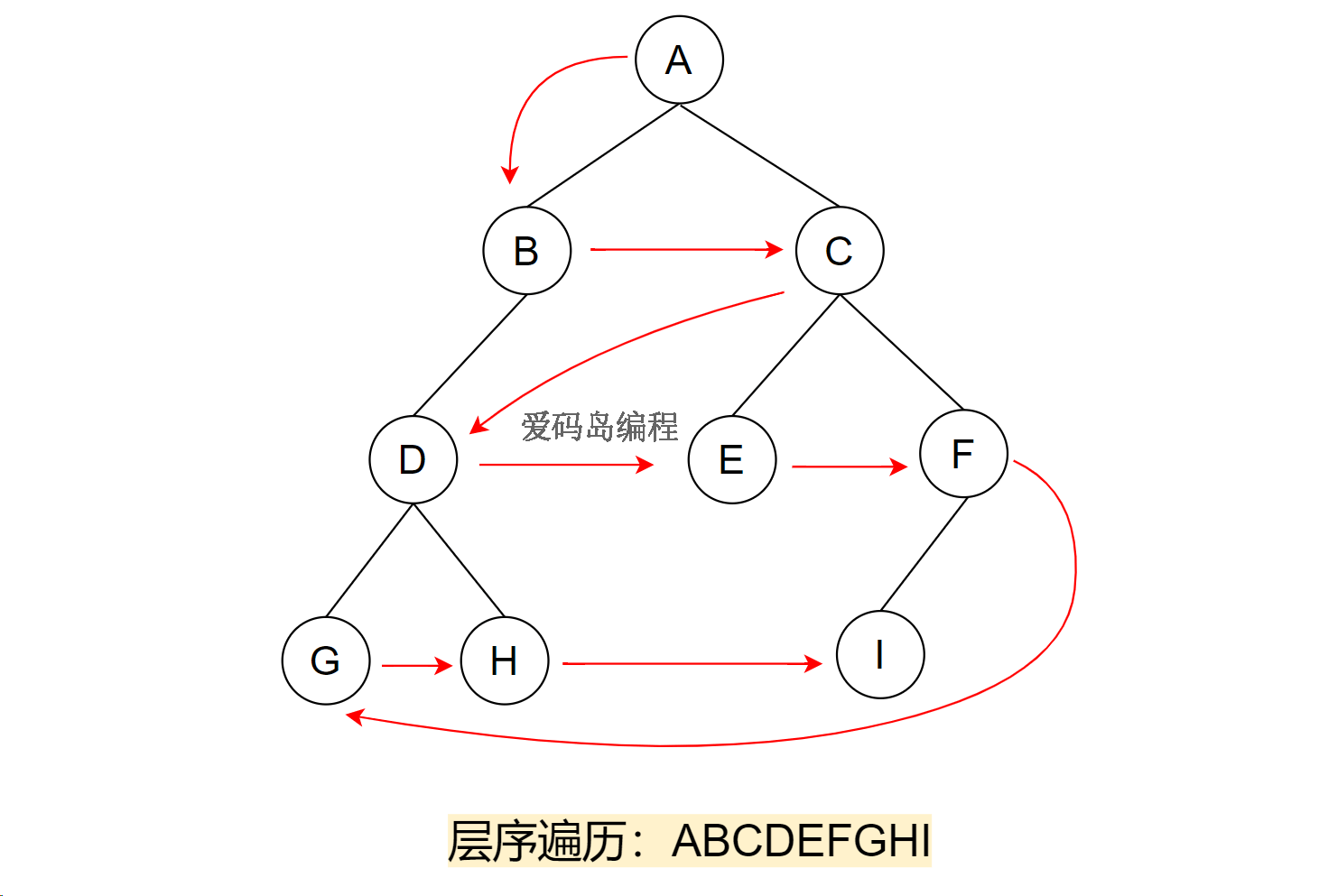
如果二叉树为空直接返回。否则依次从树的第一层开始从上至下逐层遍历，在同一层中按从左到右的顺序对结点逐个访问。

void LevelOrderTraverse(TreeNode *root) {
    if(root == NULL) {
        return;
    }
    
	queue<TreeNode *> q;//借助队列实现
    q.push(root);
    while (!q.empty()) {
        print(q.front()->data);
        if (q.front()->left != NULL) {
            q.push(q.front()->left);
        }
        if (q.front()->right != NULL) {
            q.push(q.front()->right);
        }
        q.pop();
    }
}