树是非线性数据结构,树中的结点(或节点)之间具有明确的层次关系,结点之间有分支,非常类似于真正的树。树状结构在客观世界中大量存在,如行政组织机构和人类社会的家谱等都可用树状结构形象地表示。
一、树的概念
树是n(n≥0)个结点的有限集T。T要么是空集(空树),要么是非空集。对于一棵非空树,有且仅有一个特定的称为根(root)的结点,其余结点可分为 m(m>0) 个互不相交的有限集T1, T2,..., Tn
-
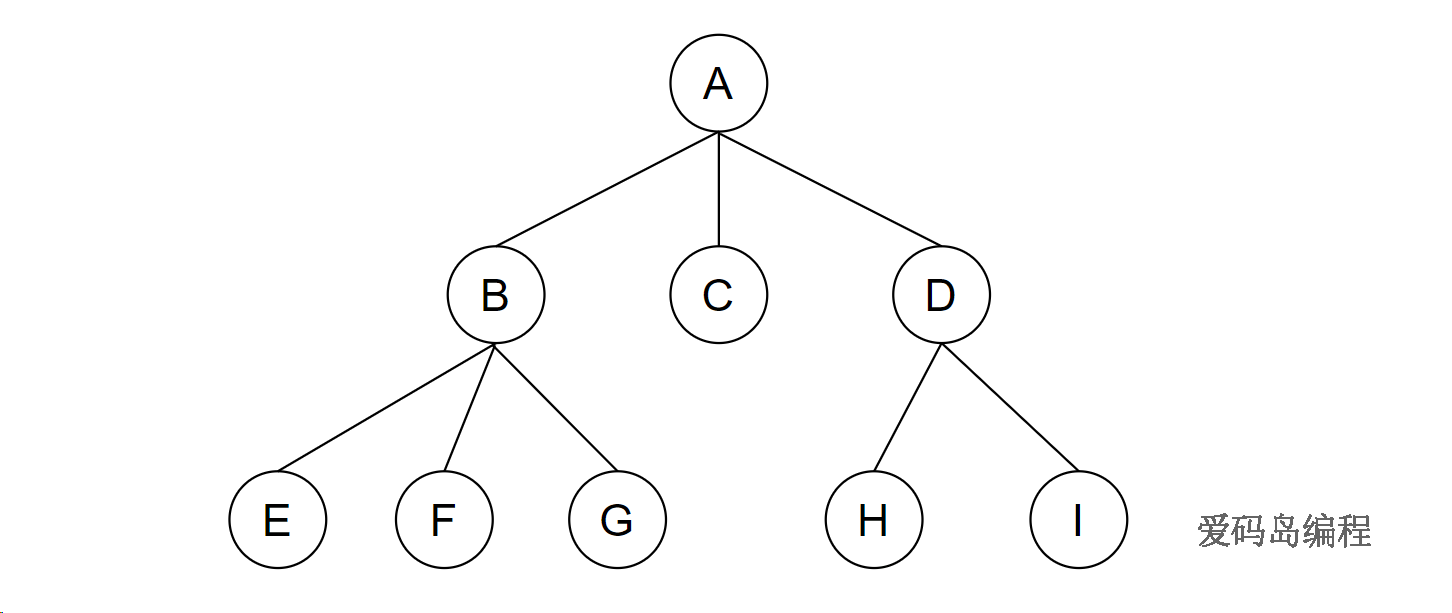
上图是一颗树,A是根结点,也就是root结点。一棵树的根结点只能有一个。
-
B、C、D分别又是一颗树,也就是有限集T1,T2,T3,他们都是A的子树。同理可以往下递归有限集T。
-
这棵树有9个结点,也就是n=9的有限集T。
-
当n=0的时候,也就是0个结点的情况,就是一颗空树。
-
一个结点拥有的子树数量称为该树结点的度(degree)。一棵树中结点最大的度称为该树的度。比如A的度是3,B的度是3,D的度是2,那么这课数的度是3。
-
度为0的结点称为叶子结点,C、E、F、G、H、I 都是叶子结点。也就是说叶子结点不能有任何子树。
-
除了根结点和叶子结点之外的结点都叫内结点,比如B,D。
-
树的深度就是结点的层次,从根结点开始记为第1层。如果某个结点在第 i 层,那么它的子树根结点在第 i+1 层。树中结点最大的层次就是该树的深度。上方这颗树的深度是3。
-
结点与结点间是有关系称谓的。孩子结点(B是A的孩子结点),父结点(A是B的父结点),兄弟结点(同一父结点下的孩子结点,B、C、D是兄弟结点)。
-
森林是m颗互不相交的树的集合。比如把根结点A删除了,那么就是三颗树组成的森林。
二、二叉树
二叉树(binary tree)是一种特殊的树,其每个结点的度都不大于2,并且每个结点的孩子结点次序不能任意颠倒。所以一颗二叉树的每个结点只能含有0、1或2个孩子。每个孩子还有左右之分,通常把左边的孩子叫做左子树,右边的孩子叫做右子树。
struct TreeNode{
int data;
TreeNode *left;
TreeNode *right;
};
二叉树的基本形态有以下5种。
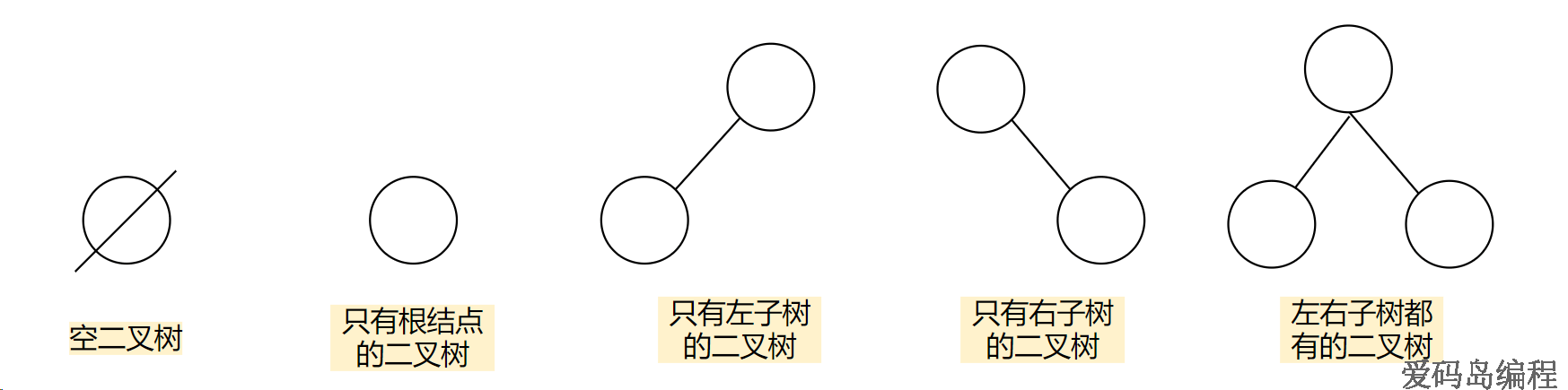
三、满二叉树和完全二叉树
满二叉树:如果一个二叉树的层数为 k,且结点总数是 2k - 1 ,则它就是满二叉树,第 k 层的结点数是2(k-1)。
完全二叉树:完全二叉树的结点数是任意的。它缺失结点是最后一行右下角某个连续的部分,即按层顺序排列从左到右是连续的,缺失右下脚连续部分。对于 k 层的完全二叉树,结点数的范围 2(k-1)-1 < n < 2k - 1
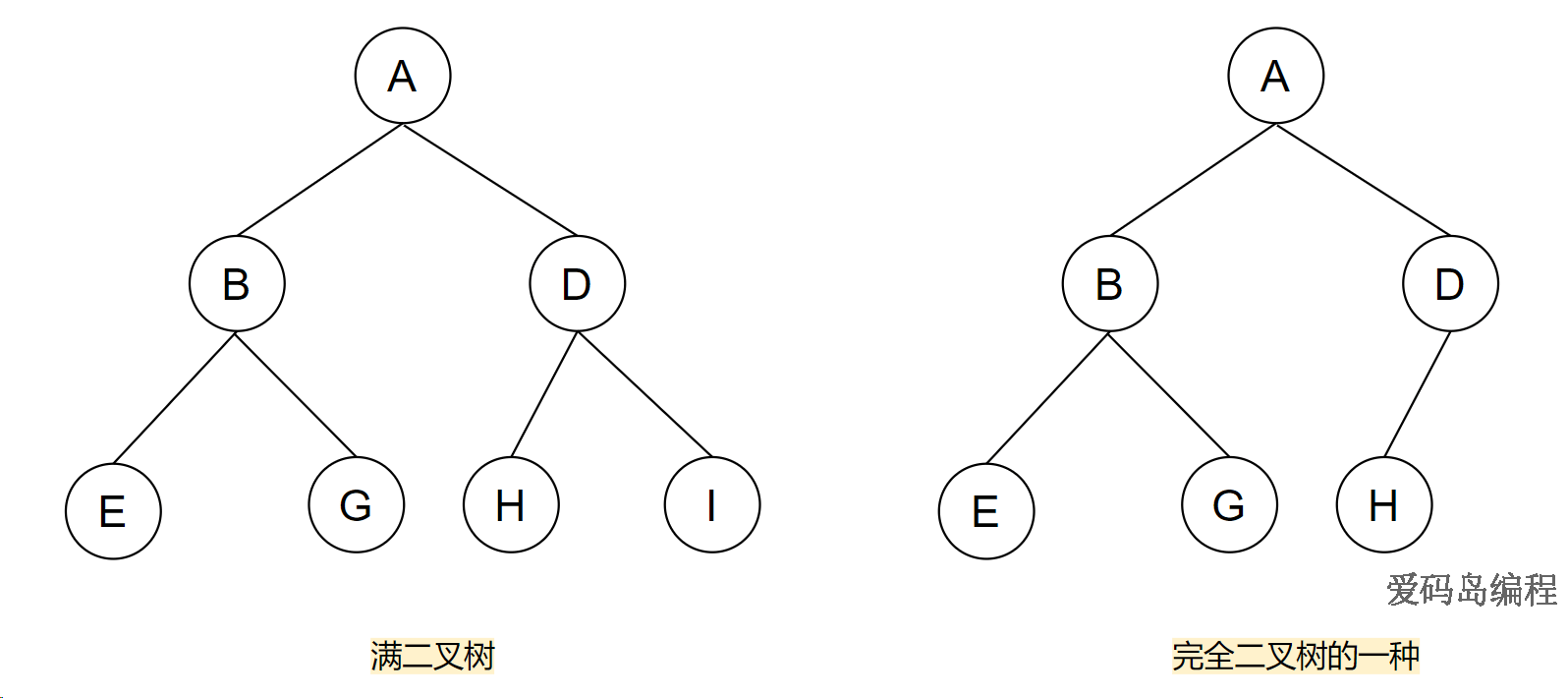
满二叉树一定是完全二叉树,而完全二叉树则不一定是满二叉树。