从图的某一顶点出发系统地访问图中所有顶点，使每个顶点都被访问一次，叫做图的遍历。

为了避免重复访问某个顶点，可以设一个标志数组visited[i]，未访问的设置为false，访问一次后设置为true。

图的遍历有两种：深度优先遍历（Depth-First Search, DFS）和广度优先遍历（Breadth-First Search, BFS），两者的时间复杂度都是O(n*n)。

一、深度优先遍历

在深度优先遍历中，从起点出发，每次尽可能沿着一条路径走到底，当到达尽头时回溯到之前的结点，继续遍历其它的结点，直到遍历完所有的结点为止。在深度优先遍历中，可以使用栈（Stack）或递归函数实现。

具体地，如果使用栈实现深度优先遍历，需要按照以下步骤进行：

1. 将起点入栈，并将其标记为已访问；

2. 如果栈不为空，从栈顶取出一个结点（访问结点），遍历该结点的邻居结点，将未访问过的邻居结点入栈；

3. 重复以上，直到栈为空为止；

那么，出栈顺序即深度优先搜索的遍历顺序，深度优先搜索可以有多种顺序。

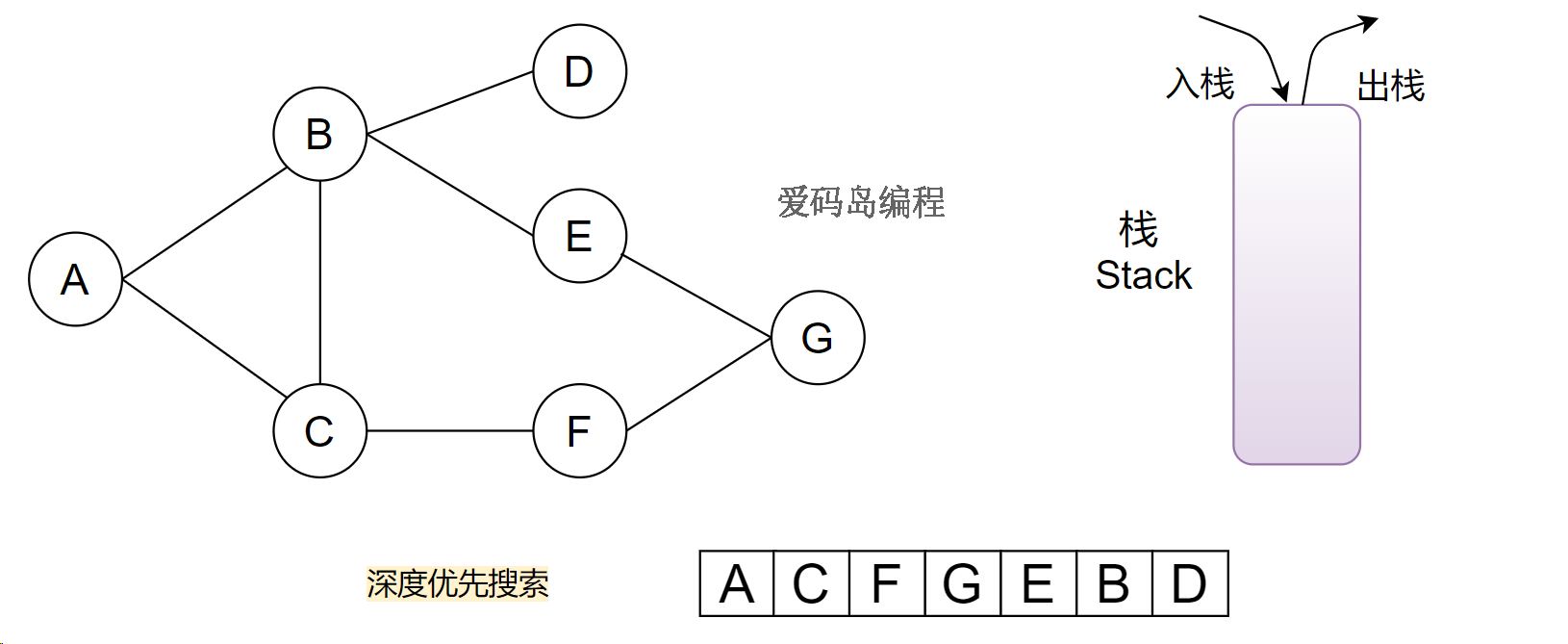
过程如下：

• A入栈，并标记A已访问。

• A在栈中，栈不为空，那么从栈顶取出一个结点（A出栈，就是访问A），遍历A的邻居结点（B和C），未访问过就入栈。C入栈B入栈（标记已访问）。

• 栈中有C、B（或B、C），不为空，重复上面步骤。

• C出栈，F入栈....

栈的特点是，从栈顶出，所以是沿着一条路径走到底；出栈可以理解为回溯到上一个结点。

二、广度优先遍历

从起点开始，首先将其加入队列中，然后从队列中取出一个结点，并将其所有未被访问过的邻居结点加入队列中，依次类推，直到队列为空。广度优先遍历的实现需要借助一个队列（Queue）数据结构。

广度优先遍历算法的具体实现步骤如下：

1. 初始化一个队列，将起始顶点加入队列中，并标记其为已访问；

2. 队列不为空，从队列中取出一个结点（访问该结点），将其所有未访问过的相邻顶点加入队列中；

3. 如果队列不为空，则重复步骤1、2，直到队列为空；

那么，出队列顺序即广度优先搜索的遍历顺序，广度优先搜索可以有多种顺序。

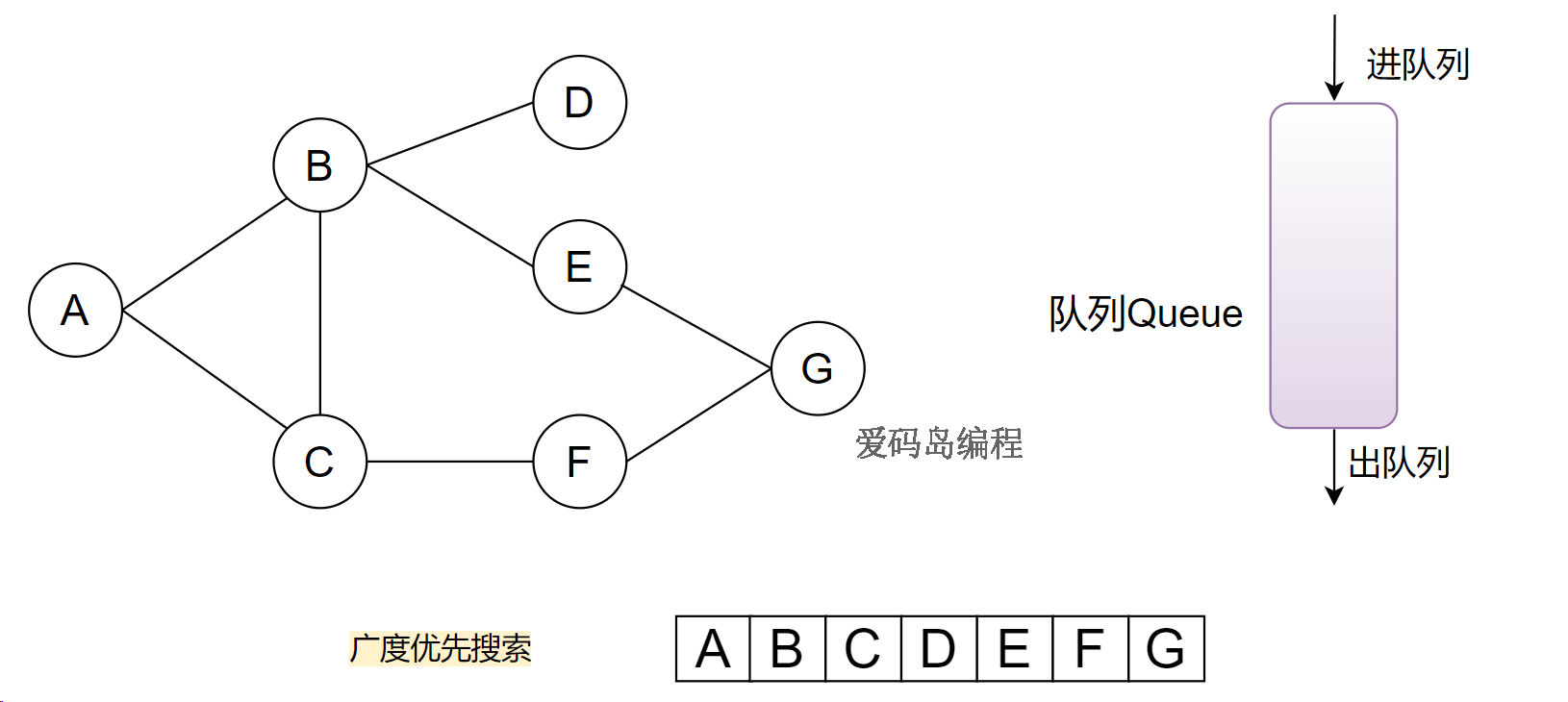
过程如下：

• A入队列，标记为已访问；

• A在队列中，队列不为空，A出队列（就是访问A），遍历A的邻居结点（B和C），未访问过就入队列。B入队列、C入队列（标记已访问）。

• 队列中有B、C（或C、B），不为空，重复上面步骤。

• D入队列、E入队列....

队列的特点是从队头出，所以是先把顶点的相邻结点全部访问完。