拓扑排序是图的算法，用于解决依赖关系和顺序性问题，确保在满足约束条件的情况下正确排序图中的顶点。

拓扑排序是一种对有向无环图（DAG：Directed Acyclic Graph）中的顶点进行线性排序的算法。

拓扑排序常用于表示任务之间的依赖关系，确保任务按照依赖关系的顺序执行。如：火车路线图、课程表、任务调度、编译器优化、依赖关系分析等领域。

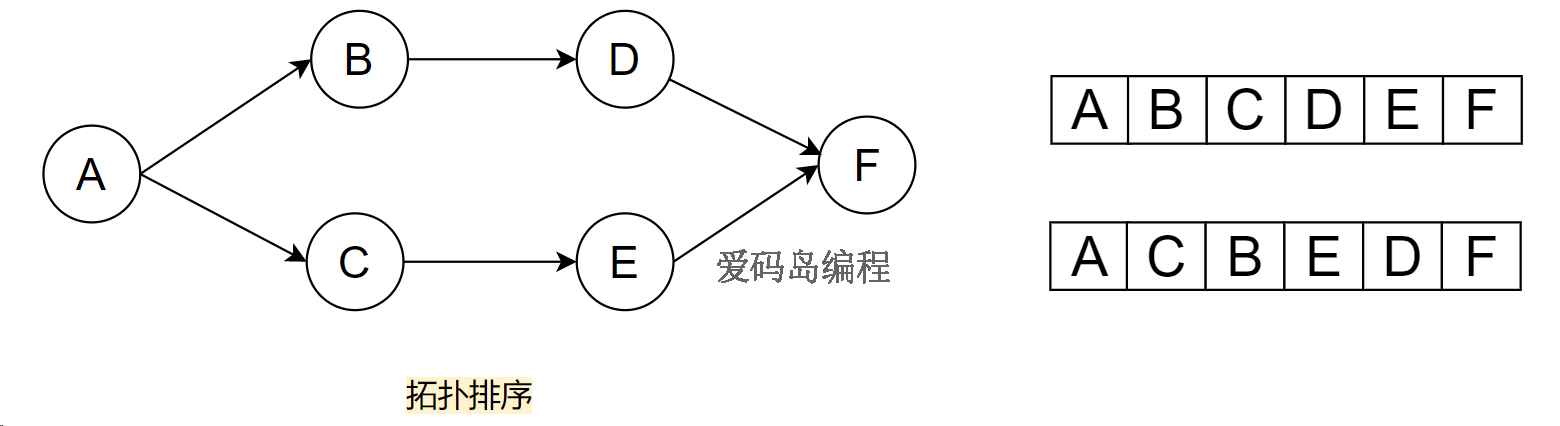
拓扑排序通常使用深度优先搜索（DFS）或广度优先搜索（BFS）算法来实现。通常，一个有向无环图可以有一个或多个拓扑排序序列。

一、如何找到有效拓扑排序？

1、找入度为0的结点，依次放到拓扑排序中

2、将该结点的出度（边）删掉

3、重复1、2步骤，完成整个图中结点的删除

二、练习题

关于拓扑排序，下列说法正确的是( )

A. 所有连通的有向图都可以实现拓扑排序

B. 对同一个图而言，拓扑排序的结果是唯一的

C. 拓扑排序中入度为0的结点总会排在入度大于0的结点的前面

D. 拓扑排序结果序列中的第1个结点一定是入度为0的结点

参考答案 D

拓扑排序是从入度为0的点开始找。

已知有向图G=(V,E)，其中V={V1,V2,V3,V4,V5,V6,V7}，E={<V1,V2>,<V1,V3>,<V1,V4>,<V2,V5>,<V3,V5>,<V3,V6>,<V4,V6>,<V5,V7>,<V6,V7>}，G的拓扑排序是( )

A. V1,V3,V4,V6,V2,V5,V7

B. V1,V3,V2,V6,V4,V5,V7

C. V1,V3,V4,V5,V2,V6,V7

D. V1,V2,V5,V3,V4,V6,V7

参考答案 A

画图演算：构造图，找出拓扑排序。