哈夫曼树也叫最优二叉树。

设二叉树有 n 个带权值的叶子结点，那么从根结点到各个叶结点的路径长度与相应结点权值的乘积的和，叫做二叉树的带权路径长度WPL(Weighted Path Length)。

一、带权路径长度WPL

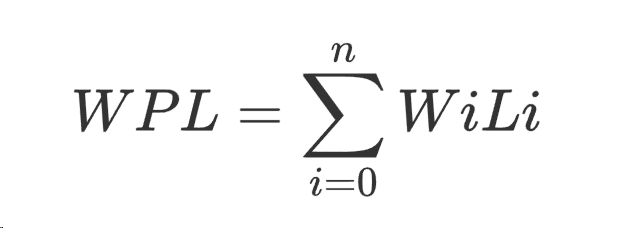
求WPL案例

• 2、3、1 分别是叶子结点的权值

• 路径长度是层数 k-1，也就是有几个路径，分别是2、2、1。

二、哈夫曼树

相同的叶子结点构造出来的不同二叉树

叶子结点的路径长度不同，得到的WPL不一样。

具有最小带权路径长度的二叉树称为哈夫曼树，也叫最优二叉树。

三、如何构造哈夫曼树

构造原则：

权值越大的叶结点越靠近根结点，权值越小的叶结点越远离根结点。

构造过程：

(1) 给定的n个权值 {W1,W2,...,Wn} 构造 n 棵只有根结点的二叉树，从而得到一个二叉树的集合 F={T1, T2, ..., Tn}

(2) 在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树（或右、左子树）构造一棵新的二叉树，这棵新的二叉树根结点的权值为其左、右子树根结点权值之和。

(3) 在集合F中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到集合F中。

(4) 重复 (2)、(3) 两步，当F中只剩下一棵二叉树时，这棵二叉树便是所要建立的哈夫曼树。

案例演示

已知权值 W={0.05, 0.29, 0.07, 0.08, 0.14, 0.23, 0.03, 0.11} ，构造一颗哈夫曼树。

我们可以转换成整数，然后做一个排序，得到 W = {3, 5, 7, 8 ,11, 14, 23, 29}

四、哈夫曼编码

规定哈夫曼树中的左分支为0，右分支为1，则从根结点到每个叶结点所经过的分支对应的 0 和1组成的序列便为该结点对应字符的编码。这样的编码称为哈夫曼编码。

哈夫曼编码属于0、1二进制编码。

哈夫曼编码的特点：权值越大的字符编码越短，反之越长。

5： 0001
3： 0000
11：001
23：01
14：100
7： 1010
8： 1011
29：11

掌握如何构造哈夫曼树和哈夫曼编码

五、练习题

假设字母表 {a,b,c,d,e} 在字符串出现的频率分别为 10%,15%,30%,16%,29%。若使用哈夫曼编码方式对字母进行不定长的二进制编码，字母 d 的编码长度为( )位。

A. 1

B. 2

C. 2或3

D. 3

参考答案 B

画图演算：先排序，再构造哈夫曼树。

假设有⼀组字符{a,b,c,d,e,f}，对应的频率分别为5%、9%、12%、13%、16%、45%。请问以下哪个选项是字符a,b,c,d,e,f分别对应的⼀组哈夫曼编码( )

A. 1111，1110, 101，100, 110, 0

B. 1010，1001，1000，011, 010, 00

C. 000，001，010，011，10，11

D. 1010，1011，110，111，00，01

参考答案 A

画图演算，构造哈夫曼树。